
ยินดีต้อนรับเข้าสู่ เว็บแทงหวยออนไลน์ที่ดีที่สุด 999LUCKY109 เว็บหวยออนไลน์ครบวงจร
ตอบโจทย์สำหรับคอหวย เว็บมาตรฐานระดับเอเซีย อันดับ 1 ในไทยตอนนี้
ยินดีต้อนรับคุณลุูกค้าที่เป็นสมาชิกทุกท่าน เข้าสู่ระบบ เว็บแทงหวยออนไลน์ 999LUCKY109 เว็บแทงหวยออนไลน์ครบวงจร มีหวยออนไลน์มากมายให้ท่านได้เลือกเล่น ระบบเว็บที่ได้มาตรฐานที่สุด ได้รับการการันตีจากประเทศเพื่อนบ้าง ด้วยระบบรักษาความปลอดภัยทีดีที่สุด ข้อมูลส่วนตัวหรือบัญชีของท่านจะถูกเก็บไว้เป็นความลับ รักษาความปลอดภัยให้ท่านแบบขั้นสูง แบบที่ว่าไม่มีใครสามารถเห็นข้อมูลของท่านเลยก็ว่าได้
แทงหวยออนไลน์ครบวงจร ต้อง 999LUCKY เท่านั้น มีหวยออนไลน์มากมายให้ท่านได้เลือกเล่น อาทิเช่น หวยรัฐบาลไทย หวยเวียดนาม(หวยฮานอย) หวยปิงปอง(หวยยี่กี) หวยลาว Huayden หวยมาเลย์ หวยหุ้นไทย หวยหุ้นต่างประเทศ และหวยอื่นอีกมากมาย ครบครัน ตอบโจทย์สำหรับนักเสี่ยงโชคทั้งหลาย ที่ชอบในการเล่นหวยออนไลน์
แทงหวย กับ 999LUCKY ท่านจะได้ประสบการณ์ใหม่ที่ดีแน่นอน เพราะเราเปิดให้บริการด้านหวยมานานกว่า 10 ปี โดยที่เราไม่เคยมีประวัตเสียด้านการเงินหรือโกงลูกค้าเลยแม้แแต่ครั้งเดียว เรามาพร้อมระบบ ฝากถอนอัตโนมัติ ฝากถอนรวดเร็วที่สุด ฝากเงินไปแล้วปรับยอดเครดิตเร็ว โดยที่ท่านไม่ต้องรอการยืนยันจากพนักงานอะไรเลย ฝากถอนโดยไม่มีขั่นต่ำ แทงหวยไม่มีขั่นต่ำ เป็นเว็บที่ใหญ่ที่สุดในไทยและเปิดให้บริการเป็นเจ้าแรกๆ ในไทยเลยก็ว่าได้
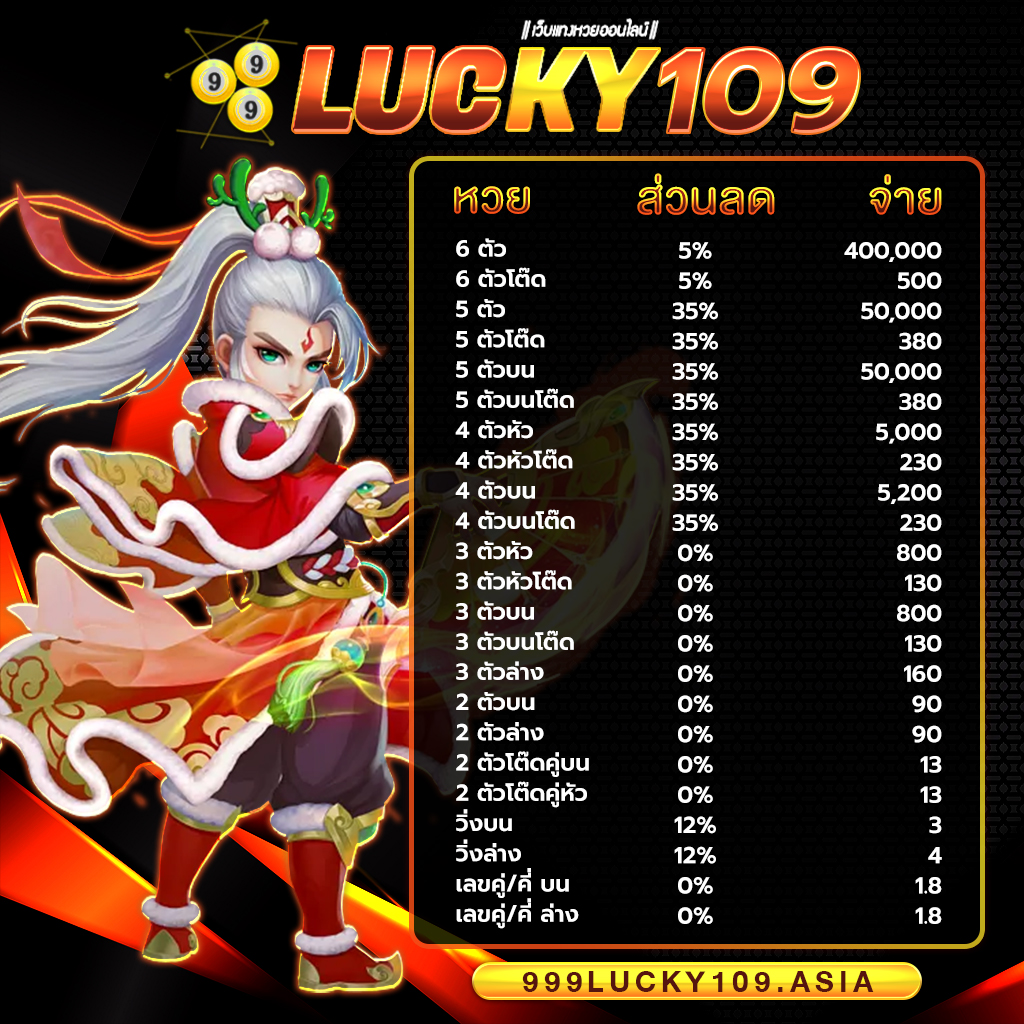
999LUCKY จ่ายจริง จ่ายเต็ม ไม่อั้น รับทุกตัว ไม่มีโกง แน่นอนครับ ถูกล้านเราก็จ่ายล้าน ได้เงินครบทุกบาททุกสตางค์ ถือว่าเว็บไซต์เราเป็น เว็บหวยออนไลน์ที่ดีที่สุดอันดับ 1ในประเทศไทย เลยก็ว่าได้ หากท่านจะเป็นนักแทงหวยที่เก่งที่สุด แนะนำ 999LUCKY เว็บ Huay ที่ดีที่สุด Hauyden เล่นแล้วรวย แล้วท่านจะรวยโดยที่ท่านไม่รู้ตัว รวยก่อนใครได้ที่ ” สมัครสมาชิก 999LUCKY ” ไม่เสียค่าใช้จ่ายแม้แต่บาทเดียว บริการประทับใจ ใส่ใจดูแลท่านตลอด 24 ซม. แล้วท่าจะไม่ผิดหวังแน่นอนถ้าเลือก 999LUCKY เว็บแทงหวยออนไลน์ที่ดที่สุด มาตรฐานที่สูงในเอเซีย
ระบบรักษาความปลอดภัยที่ดีที่สุด ต้อง 999LUCKY ที่นี้ที่เดียวเท่านั้น
เว็บแทงหวยออนไลน์ 999LUCKY เป็นเว็บแทงหวยออนไลน์ที่มีระบบรักษาความปลอดภัยที่ดีที่สุด มีมาตรฐานสูง หายห่างเรื่องข้อมูลส่วนตัวหรือข้อมูลบัญชีธนาคารของท่าน หายห่วงเรื่องโดนแฮก ทางเว็บไซต์เราจะเก็บไว้เป็นความลับอย่างดี ระดับที่ว่าไม่มีใครสามารถรู้ถึงข้อมูลของท่านเลยก็ว่าได้ สบายใจได้ ไม่ต้องกังวลเรื่องโดนยักยอกเงิน ท่านจะได้เงินครบทุกบาททุกสตางค์ เรากล้าการันตีได้ว่าถ้ามีปัญหาอะไรเราจะรับผิดชอบให้ลูกค้าทุกท่านให้หมด ไม่มีเว็บไซต์ไหน ใจถึงเท่ากับเราอีกแล้วครับ เพราะฉะนั่น มั่นใจได้ถึงระบบรักษาความปลอดภัยของเราได้เลย แทงหวย กับ 9999LUCKY การเงิน มั่นคง ปลอดภัย 100% แน่นอนครับ
- ระบบป้องกันการแฮกที่ทันสมัยที่สุด โดย โปรแกรมเมอร์ที่เก่งที่สุดในบรรดา เว็บแทงหวยออนไลน์
- ระบบ Server รวดเร็วที่สุดปลอดภัยที่สุดด้วย Server ส่วนตัว
- สำรองข้อมูลให้ท่านตลอดเวลา หายห่วงเรื่องการเงินและบัญชีของท่าน
- ระบบเข้ารหัสข้อมูลลูกค้า ไม่สามารถแฮกได้ง่ายๆ
ทำไมต้องแทงหวยออนไลน์กับ 999LUCKY
- มีหวยออนไลน์ครบวงจร ให้ท่านเลือกเล่นมากมาย ไม่น่าเบื่อ
- ออกหวยถี่ที่สุด ออกบ่อย เรียกกันได้เลยว่าเล่นได้ทั้งวันทั้งคืน
- จ่ายจริง ไม่อั้น ไม่หัก จ่ายเต็ม ไม่เคยมีประวัติการโกงลูกค้ามาก่อน
- ข้อมูลส่วนตัวและบัญชีของท่าน จะถูกเก็บไว้เป็นความลับ
- ผลหวยออกเร็ว ตรวจหวยฟรี ได้ก่อนใคร เร็วกว่าเว็บไหนๆ
- หากมีปัญหาหรือข้อสงสัย สามารถ “ติดต่อทางทีมงาน 999LUCKY” ได้ตลอด 24 ซม.
เว็บแทงหวยออนไลน์ครบวงจรที่ดีที่สุด 999LUCKY เว็บแทงหวยมาตรฐานระดับเอเซีย
999LUCKY เว็บแทงหวยออนไลน์ ที่ครองใจคนไทยมานานกว่า 10 ปี เพราะเราบริการด้วยหัวใจ
ฝากถอนด้วยระบบอัตโนมัติ ฝากถอนโดยไม่มีขั่นต่ำ ฝากถอนรวดเร็วที่สุด ของเว็บหวยออนไลน์
สมัครสมาชิก กับ 999LUCKY ท่านจะรับโปรโมชั่นหรือโบนัสและสิทธิพิเศษมากมาย รอท่านอยู่ !!
หากเกิดปัญหาหรือข้อสงสัย ระหว่าการใช้งานสามารถ ติดต่อทีมงาน เราได้ตลอด 24 ซม.
สามารถ ตรวจหวย หรือ ตรวจย้อนหลัง ได้ที่ 999LUCKY รวดเร็วกว่าใคร แม่นยำที่สุด

